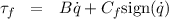
The Robot and mRobot classes

2.3 The Robot and mRobot classes

The Robot and mRobot classes are composed of the following data elements:

the number of degree of freedom n (int dof);
the gravity acceleration vector (-g) expressed in the base frame
(ColumnVector gravity);
one array of dimension n of Link object elements (Link *links);

and the member functions providing the different algorithms implementation (see tables 2.2–2.17).

The Link class (see table 2.1) encapsulates all the data and functionality required to characterize a single “link” as it is defined by Denavit and Hartenberg (standard notation [3], or modified notation [4]). It is initialized by providing the joint type (int joint_type: revolute=0, prismatic=1) and the parameters θ, d, a, α (Real theta, d, a, alpha) and a boolean value Bool DH (true=standard false=modified) It also contains the inertial parameters data: mass m (Real m), center of mass position vector r (ColumnVector r) and inertia tensor matrix I_c (Matrix I). In this case, r is given with respect to the link coordinate frame and I_c is with respect to a coordinate frame parallel to the link coordinate frame and located at the center of mass of m. The dynamic model takes into account the motors inertia, gear ratio and frictions. The values Im and Gr representing respectively the motors rotor inertia I_m and gear ratio G_r; B and Cf representing respectively the motors viscous B and Coulomb friction C_f coefficients:

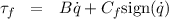
τf = B q˙+ Cfsign(˙q)

Table 2.1: The Link class data parameters



Kinematic		Inertial		Motor


int	joint_type	Real	m	Real	Im
Real	theta, d, a, alpha	ColumnVector	r	Real	Gr
Real	joint_offset	Matrix	I	Real	B
ColumnVector	p			Real	Cf
Matrix	R,
Bool	DH
Real	theta_min, theta_max
Real	joint_offset

On initialization, the constructor sets up the matrices R and p such that

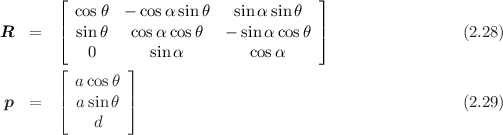
⌊ cos θ - cosαsinθ sinα sin θ ⌋ | | R = ⌈ sin θ cos αcosθ - sinα cosθ ⌉ (2.28) 0 sin α cos α ⌊ acosθ ⌋ p = | asin θ | (2.29) ⌈ ⌉ d

for the standard D-H notation and

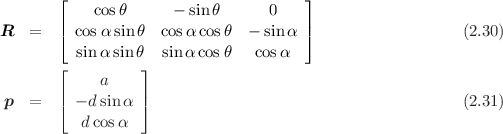
⌊ cosθ - sin θ 0 ⌋ | | R = ⌈ cos αsinθ cosα cosθ - sin α ⌉ (2.30) ⌊ sin αsinθ⌋ sinα cosθ cosα a p = |⌈ - d sinα |⌉ (2.31) d cosα

for the modified D-H notation.

If the link corresponds to a revolute (prismatic) joint, then only θ (d) can be changed after the link definition. This is done through the member function transform which sets the new value of q (θ or d) and updates the matrices R and p which compose the link homogeneous transform:

[ ] T = R p (2.32) 0 1

Only the changing elements are computed since the data of an instance of a class is persistent throughout the scope of definition of the instance (see [5]). In standard notation, the elements (3,2) and (3,3) of R provide storage for cosα and sinα which are computed only once. In modified notation, the elements (3,3) and (2,3) of R provide storage for cosα and sinα. So as to make the implementation faster, only the elements of R and p involving θ (d) are updated with a revolute (prismatic) joint.

2.3.1 Robot and mRobot object initialization

The Robot and mRobot classes provide a default constructor that creates a 1 dof robot. A n_dof × 19 matrix containing the kinematic and inertial parameters (as for the Robot class) can be supplied upon initialization. A n_dof × 19 matrix containing the kinematic and inertial parameters (as for the Robot class) can be supplied along with a n_dof × 4 matrix providing the motors inertia, gear ratio and friction coefficients. A n_dof × 23 matrix (kinematic, inertial and motor parameters) can also be used. The structure of the initialization matrix is:

Column	Variable	Description

1	σ	joint type (revolute=0, prismatic=1)
2	θ	Denavit-Hartenberg parameter
3	d	Denavit-Hartenberg parameter
4	a	Denavit-Hartenberg parameter
5	α	Denavit-Hartenberg parameter
6	θ_min	minimum value of joint variable
7	θ_max	maximum value of joint variable
8	θ_off	joint offset
9	m	mass of the link
10	c_x	center of mass along axis x
11	c_y	center of mass along axis y
12	c_z	center of mass along axis z
13	I_xx	element xx of the inertia tensor matrix
14	I_xy	element xy of the inertia tensor matrix
15	I_xz	element xz of the inertia tensor matrix
16	I_yy	element yy of the inertia tensor matrix
17	I_yz	element yz of the inertia tensor matrix
18	I_zz	element zz of the inertia tensor matrix
19	I_m	motor rotor inertia
20	Gr	motor gear ratio
21	B	motor viscous friction coefficient
22	C_f	motor Coulomb friction coefficient
23	immobile	flag for the kinematics and inverse kinematics
		(if true joint is locked, if false joint is free)

constructors

Syntax

Standard notation:

Robot(const int ndof=1);
Robot(const Matrix & initrobot);
Robot(const Matrix & initrobot, const Matrix & initmotor);
Robot(const Robot & x);
Robot(const string & filename, const string & robotName);

Modified notation:

mRobot(const int ndof=1);
mRobot(const Matrix & initrobot_motor);
mRobot(const Matrix & initrobot, const Matrix & initmotor);
mRobot(const mRobot & x);
mRobot(const string & filename, const string & robotName);

Description

Robot and mRobot object constructors, copy constructor and equal operator.

Return Value

None

get_q, get_qp, get_qpp

Syntax

ReturnMatrix get_q(void);
Real get_q(const int i);
ReturnMatrix get_qp(void);
Real get_qp(const int i);
ReturnMatrix get_qp(void);
Real get_qp(const int i);

Description

These functions return a column vector containing the joint variables (get_q), velocities (get_qp) or accelerations (get_qpp) when called with no argument. It returns the scalar value for the i^th joint variable when called with an integer argument.

Return Value

ColumnVector or Real

set_q, set_qp, set_qpp

Syntax

void set_q(const ColumnVector & q);
void set_q(const Matrix & q);
void set_q(const Real q, const int i);
void set_qp(const ColumnVector & qp);
void set_qp(const Matrix & qp);
void set_qp(const Real qp, const int i);
void set_qpp(const ColumnVector & qpp);
void set_qpp(const Matrix & qpp);
void set_qpp(const Real qpp, const int i);

Description

These functions set the joint variables (velocities or accelerations) or the i^th joint variable (velocity or acceleration) to q (qp or qpp).

Return Value

None

2.3.2 Kinematics

The forward kinematic model defines the relation:

0T n = G (q) (2.33)

where ⁰T_n is the homogeneous transform representing the position and orientation of the manipulator tool (frame n) in the base frame 0. The inverse kinematic model is defined by

-1 0 q = G (T n) (2.34)

In general, this equation allows multiple solutions.

inv_kin

Syntax

ReturnMatrix inv_kin(const Matrix & Tobj, const int mj = 0);
ReturnMatrix inv_kin(const Matrix & Tobj, const int mj,
const int endlink, bool & converge);

Description

The inverse kinematic model is computed using a Newton-Raphson technique. If mj == 0, it is based on the following [6]:

0 * 0 0 T n(q ) = Tn(q + δq) ≈ Tn (q )δT (δq) = Tobj (2.35) δT (δq ) = (0Tn(q))-1T obj = I + Δ (2.36) ⌊ ⌋ | 0 - δz δy dx | Δ = || δz 0 - δx dy || (2.37) ⌈ - δy δx 0 dz ⌉ 0 0 0 0 n [ ]T δχ = dx dy dz δx δy δz (2.38) nδχ ≈ nJ(q)δq (2.39)

If mj == 1, it is based on the following Taylor expansion [6, 7]:

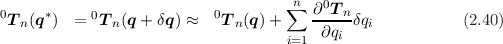
0 * 0 0 ∑n ∂0T-n T n(q ) = T n(q + δq) ≈ Tn (q )+ ∂qi δqi (2.40) i=1

The function dTdqi computes these partial derivatives.

Given the desired position represented by the homogeneous transform Tobj, this function return the column vector of joint variables that is corresponding to this position. On return, the value converge is true if the procedure has converge to values that give the correct position and false otherwise.

Note: mj == 0 is faster (≈ 1.8×) than mj == 1. Also, mj == 1 might converge when mj == 0 does not.

Return Value

ColumnVector

inv_kin_rhino

Syntax

ReturnMatrix inv_kin_rhino(const Matrix & Tobj,
bool & converge)

Description

This function performs the Rhino robot inverse kinematics.

Return Value

ColumnVector

inv_kin_puma

Syntax

ReturnMatrix inv_kin_puma(const Matrix & Tobj,
bool & converge)

Description

This function performs the Puma robot inverse kinematics.

Return Value

ColumnVector

jacobian

Syntax

ReturnMatrix jacobian(const int ref=0);
ReturnMatrix jacobian(const int endlink, const int ref)const;

Description

The manipulator Jacobian defines the relation between the velocities in joint space 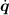and in the Cartesian space 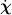expressed in frame i:

i ˙χ = iJ (q)˙q (2.41)

or the relation between small variations in joint space δq and small displacements in the Cartesian space δχ:

iδχ ≈ iJ (q)δq (2.42)

The manipulation Jacobian expressed in the base frame is given by (see [8])

[ ] 0J(q) = 0J 1(q) 0J2(q) ⋅⋅⋅ 0J n(q ) (2.43)

with

[ i-1 ] 0J (q) = zi- 1 × pn for a revolute joint (2.44) i zi-1 [ ] 0Ji(q) = zi- 1 for a prismatic joint (2.45) 0

where z_i-1 and ^i-1p_n are expressed in the base frame and × is the vector cross product. Expressed in the i^th frame, the Jacobian is given by

[ (0R )T 0 ] iJ(q) = i 0 T 0J (q) (2.46) 0 (Ri )

This function returns ⁱJ(q) (i = 0 when not specified) for the endlink (last link when not specified).

Return Value

Matrix

jacobian_dot

Syntax

ReturnMatrix jacobian_dot(const int ref=0);

Description

The manipulator Jacobian time derivative can be used to compute the end effector acceleration due to joints velocities [9]:

i¨x = i ˙J(q,q˙)q˙ (2.47)

The Jacobian time derivative expressed in the base frame is given by [9]

[ ] 0 ˙J(q,q˙) = 0J˙1(q, ˙q) 0 ˙J2(q, ˙q) ⋅⋅⋅ 0 ˙Jn (q,q˙) (2.48)

with

[ ] 0 ˙ ωi- 1 × zi Ji(q, ˙q) = ωi-1 ×i- 1 pn + zi ×i- 1 ˙pn for a revolute jo(i2n.t49) [ ] 0 ˙J (q, ˙q) = 0 for a prismatic joint (2.50) i 0

where z_i and ^i-1p_n are expressed in the base frame and × is the vector cross product. Expressed in the i^th frame, the Jacobian time derivative is given by

[ ] (0Ri)T 0 i ˙J(q, ˙q) = 0 (0R )T 0 ˙J(q,q˙) (2.51) i

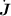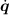This function returns ⁱ(q,)(i=0 when not specified).

Return Value

Matrix

jacobian_DLS_inv

Syntax

ReturnMatrix jacobian_DLS_inv(const Real eps, const Real lambda_max,
const int ref=0);

Description

This function returns the inverse Jacobian Matrix for 6 dof manipulator based on the Damped Least-Squares scheme [10]. Using the singular value decomposition, the Jacobian matrix is

6 J = ∑ σ u vT (2.52) i=1 i i i

where v_i and u_i are the input and output vectors, and σ_i are the singular values ordered so that σ_i ≥ σ₂ ≥ ⋅⋅⋅

σ_r ≥ 0, with r being the rank of J. Based on the Damped Least-Squares the inverse Jacobian can be written as

- 1 ∑6 --σi--- T J = σ2i + λ2 viu i (2.53) i=1

where λ is the damping factor. A singular region can be selected on the basis of the smallest singular value of J. Outside the region the exact solution is returned, while inside the region a configuration-varying damping factor is introduced to obtain the desired approximate solution. This region is defined as

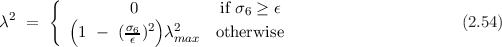
{ 2 ( 0 ) if σ6 ≥ ϵ λ = 1 - (σ6ϵ )2 λ2max otherwise (2.54)

Return Value

Matrix

kine

Syntax

void kine(Matrix & Rot, ColumnVector & pos);
void kine(Matrix & Rot, ColumnVector & pos, const int j);
ReturnMatrix kine(void);
ReturnMatrix kine(const int j);

Description

The forward kinematic model is provided by implementing the following recursion:

0Ri = 0Ri-1i-1Ri (2.55) 0p = 0p + 0R p (2.56) i i-1 i-1 i

where

[ 0 0 ] 0T = Ri pi (2.57) i 0 1

The overloaded function kine can return the orientation and position or the equivalent homogeneous transform for the last (if not supplied) or the i^th link. For example:

Robot myrobot(init_matrix);
Matrix Thomo, R;
ColumnVector p;
/* forward kinematics up to the last link */
Thomo = myrobot.kine();
/* forward kinematics up to the 2nd link */
Thomo = myrobot.kine(2);
/* forward kinematics up to the last link, outputs R and p */
myrobot.kine(R,p);
/* forward kinematics up to the 2nd link, outputs R and p */
myrobot.kine(R,p,2);

are valid calls to the function kine.

Return Value

Matrix or None (in this case Rot and pos are modified on output)

kine_pd

Syntax

ReturnMatrix kine_pd(const int ref=0);
void kine_pd(Matrix & Rot, ColumnVector & pos,
ColumnVector & pos_dot, const int ref=0);

Description

The forward kinematic model is provided by implementing the following recursion (similar to kine):

0Ri = 0Ri-1i-1Ri (2.58) 0p = 0p + 0Ri -1p (2.59) i i-1 i

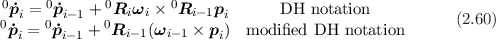
0 0 0 0 0p˙i = 0˙pi- 1 + 0Ri ωi × Ri -1pi DH notation (2.60) ˙pi = p˙i- 1 + Ri- 1(ωi- 1 × pi) modified DH notation

where

[ 0 0 ] 0T i = Ri pi (2.61) 0 1

Return Value

Matrix or None (in this case Rot, pos pos_dot are modified on output)

dTdqi

Syntax

void dTdqi(Matrix & dRot, ColumnVector & dp, const int i);
ReturnMatrix dTdqi(const int i);

Description

This function computes the partial derivatives:

∂0T ----n = 0Ti-1Qi i-1Tn (2.62) ∂qi

in standard notation and

0 ∂-T-n = 0TiQ iTn (2.63) ∂qi i

in modified notation, with

⌊ ⌋ | 0 - 1 0 0 | Qi = || 1 0 0 0 || for a revolute joint (2.64) ⌈ 0 0 0 0 ⌉ 0 0 0 0 ⌊ 0 0 0 0 ⌋ | | Qi = || 0 0 0 0 || for a prismatic joint (2.65) ⌈ 0 0 0 1 ⌉ 0 0 0 0

Return Value

Matrix or None (in this case dRot and dp are modified on output)

2.3.3 Dynamics

The robotics manipulator dynamic model is given by (see appendix A or [4])

τ = D (q)¨q + C (q,q˙)+ G (q) (2.66)

acceleration

Syntax

ReturnMatrix acceleration(const ColumnVector & q,
                          const ColumnVector & qp,
                          const ColumnVector & tau);

ReturnMatrix acceleration(const ColumnVector & q,
                          const ColumnVector & qp,
                          const ColumnVector & tau_cmd,
                          const ColumnVector & Fext,
                          const ColumnVector & Next)

Description

This function computes 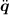from q, 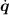and τ which is the forward dynamics problem. Walker and Orin [11] presented methods to compute the inverse dynamics. A simplified RNE version computing

τ = D (q)¨q (2.67)

is implemented in the function torque_novelocity. By evaluating this equation n times, one can compute D(q) (the inertia function), use the full RNE to compute C(q,

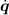) + G(q) and then solve the equation :

¨q = D - 1(q) [τ - C (q,˙q)- G (q)] (2.68)

Return Value

ColumnVector

inertia

Syntax

ReturnMatrix inertia(const ColumnVector & q);

Description

This function computes the robot inertia matrix D(q). A simplified RNE version computing

τ = D (q)¨q (2.69)

is implemented in the function torque_novelocity. By evaluating this equation n times, one can compute D(q).

Return Value

Matrix

torque

Syntax

ReturnMatrix torque(const ColumnVector & q,
                    const ColumnVector & qp,
                    const ColumnVector & qpp);

ReturnMatrix torque(const ColumnVector & q,
                    const ColumnVector & qp,
                    const ColumnVector & qpp,
                    const ColumnVector & Fext,
                    const ColumnVector & Next);

Description

This function computes τ from q, 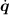and 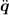which is the inverse dynamics problem. The recursive Newton-Euler (RNE) formulation is one of the most computationally efficient algorithm [12, 13] used to solve this problem (see appendix A). The second form allows the inclusion the contribution of a load applied at the last link.

Return Value

ColumnVector

torque_novelocity

Syntax

ReturnMatrix torque_novelocity(const ColumnVector & q,
                               const ColumnVector & qpp);

ReturnMatrix torque_novelocity(const ColumnVector & q,
                               const ColumnVector & qpp,
                               const ColumnVector & Fext,
                               const ColumnVector & Next);

Description

This function computes τ from q and 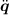when 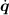= 0 and gravity is set to zero.

Return Value

ColumnVector

G and C

Syntax

ReturnMatrix G();
ReturnMatrix C();

Description

The function G() computes τ from the gravity effect, while C() computes τ from the Coriolis and centrifugal effects.

Return Value

ColumnVector for G and C

2.3.4 Linearized dynamics

Murray and Neuman [13] have developed an efficient recursive linearized Newton-Euler formulation that can be used to compute (see appendix A)

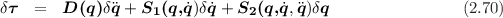
δτ = D (q)δ¨q + S (q,˙q)δ˙q + S (q,˙q,¨q)δq (2.70) 1 2

delta_torque

Syntax

void delta_torque(const ColumnVector & q,
                  const ColumnVector & qp,
                  const ColumnVector & qpp,
                  const ColumnVector & dq,
                  const ColumnVector & dqp,
                  const ColumnVector & dqpp,
                  ColumnVector & torque,
                  ColumnVector & dtorque);

Description

This function computes

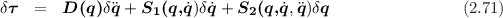
δτ = D (q)δ¨q + S (q,˙q)δ˙q + S (q,˙q,¨q)δq (2.71) 1 2

Return Value

None (torque and dtorque are modified on output)

dq_torque

Syntax

void dq_torque(const ColumnVector & q,
               const ColumnVector & qp,
               const ColumnVector & qpp,
               const ColumnVector & dq,
               ColumnVector & torque,
               ColumnVector & dtorque);

Description

This function computes

S2 (q,q˙,q¨)δq (2.72)

Return Value

None (torque and dtorque are modified on output)

dqp_torque

Syntax

void dqp_torque(const ColumnVector & q,
                const ColumnVector & qp,
                const ColumnVector & dqp,
                ColumnVector & torque,
                ColumnVector & dtorque);

Description

This function computes

S1 (q,q˙)δq˙ (2.73)

Return Value

None (torque and dtorque are modified on output)

dtau_dq

Syntax

ReturnMatrix dtau_dq(const ColumnVector & q,
const ColumnVector & qp,
const ColumnVector & qpp);

Description

This function computes

∂τ --- = S2(q,˙q,¨q) (2.74) ∂q

Return Value

Matrix

dtau_dqp

Syntax

ReturnMatrix dtau_dqp(const ColumnVector & q,
const ColumnVector & qp);

Description

This function computes

∂τ --˙ = S1(q,˙q) (2.75) ∂ q

Return Value

Matrix

perturb_robot

Syntax

void perturb_robot(Robot_basic & robot, const double f = 0.1);

Description

This function, which is not a member of any class, modifies randomly the robot parameters. The parameter variation in percentage is described by f.

Return Value

None

[next] [prev] [prev-tail] [front] [up]