
The Quaternion class deals with quaternions. Unit quaternions are used to represent rotations. It is composed of two elements: a scalar s (Real s_) and a vector v (ColumnVector v_) representing a quaternion (see[1]).

An object of this class can be initialize with no parameter (s = 1 and v = 0), from an other unit quaternion, from an angle of rotation around a unit vector, from a rotation matrix, from a quaternion object or from the four components of a quaternion. The constructors does not guarantee that quaternions will be unit.
Quaternion object constructors, copy constructor and equal operator.
None
The operators +, -, * and ∕ for quaternion are implemented. The operators * and ∕ will generate unit quaternions only if the quaternions involve are unity.
Quaternion
Compute the conjugate of the quaternion (or the inverse if it’s a unit quaternion). The conjugate is defined as

Quaternion
A unit quaternion can be represented by q = cos(θ) + usin(θ). Euler’s identity for complex numbers generalizes to quaternions exp(uθ) = cos(θ) + usin(θ), where exp(x) is replace by exp(uθ) and uu is replace by -1. With this identity we obtain the exponential of the quaternion q = (0,θv), where q is not necessary a unit quaternion. It is then possible to define the logarithm and the power of a unit quaternion [2].
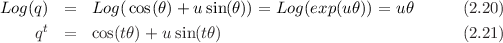
Quaternion for exp, Log
Compute the dot product of quaternions.
Real
The quaternion time derivative is obtain from the quaternion propagation law [2].


The choice of reference system (base or body) for w is assign by sign. A value of 1 is for base frame while -1 is for body frame.
Quaternion for dot
Matrix for E
unit() makes the quaternion a unit quaternion, norm() computes and returns the norm of the quaternion. norm_sqr() computes and returns the square norm of the quaternion.
Quaternion for unit()
Real for norm() and norm_sqr()
The functions s() and v() returns one of the components of a quaternion (s or v), while set_s() and set_v() can assign a value to one of the components.
None for set_s() and set_v()
Real for s()
Matrix for v()
Returns a rotation matrix from the quaternion (R() returns a 3 × 3 matrix and T() returns a 4 × 4 matrix).
Matrix
Omega is not a member function of the class Quaternion. The function returned the angular velocity obtain from a quaternion and it’s time derivative. Like the member function dot, it use the quaternions propagation law [2].
ColumnVector
Slerp stands for Spherical Linear Interpolation. Slerp is not a member function of the class Quaternion. The quaternions q0 and q1 needs to be unit quaternions. It returns a unit quaternion. As the parameter t uniformly varies between 0 and 1, the values q(t) are required to uniformly vary along the circular arc from q0 to q1.
It is customary to choose the sign G on q1 so that q0 ⋅ Gq1 ≥ 0 (the angle between q0 and Gq1 is acute). This choice avoids extra spinning caused by the interpolated rotations [2]. For unit quaternions Slerp is defined as
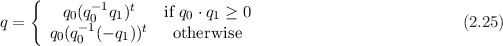
Quaternion
Slerp_prime represent the Slerp derivative. Slerp_prime is not a member function of the class Quaternion. The quaternions q0 and q1 needs to be unit quaternions. It does not necessary returns a unit quaternion.
It is customary to choose the sign G on q1 so that q0 ⋅ Gq1 ≥ 0 (the angle between q0 and Gq1 is acute). This choice avoids extra spinning caused by the interpolated rotations [2]. For unit quaternions Slerp is defined as
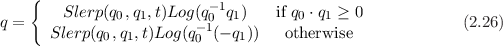
Quaternion
Squad stands for Spherical Cubic Interpolation. Squad is not a member function of the class Quaternion. The quaternions p, a, b and r needs to be unit quaternions. It returns a unit quaternion.
Squad uses an iterative of three slerps. Suppose four quaternions, p, a, b and r as the ordered vertices of quadrilateral. Interpolate c along p to q using slerp and d along a to b also using slerp. Now interpolate q along c to d [2]. Squad is defined as
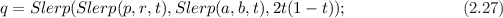
Quaternion
Squad_prime represent the Squad derivative. Squad_prime is not a member function of the class Quaternion.
Quaternion