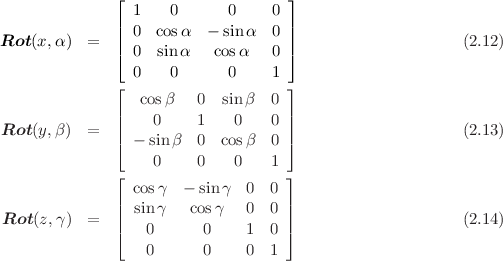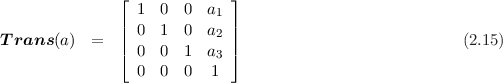3D homogeneous transforms

2.1 3D homogeneous transforms

In this section, functions dealing with 4 × 4 homogeneous transform matrices are described.

eulzxz

Syntax

ReturnMatrix eulzxz(const ColumnVector & a);

Description

Given a column vector a

⌊ γ1 ⌋ | β | (2.1) ⌈ ⌉ γ2

this function returns the homogeneous transform matrix given by

Rot (z,γ1)Rot(x,β )Rot (z,γ2) (2.2)

Note: the column vector a must have a length of at least 3. Only the first 3 elements are used.

Return Value

Matrix

ieulzxz

Syntax

ReturnMatrix ieulzxz(const Matrix & R);

Description

Given a homogeneous transform matrix R, this function returns a column vector

⌊ γ ⌋ | 1 | ⌈ β ⌉ (2.3) γ2

such that the 3 × 3 rotation bloc of the matrix

Rot (z,γ1)Rot(x,β )Rot (z,γ2) (2.4)

is equal to the 3 × 3 rotation bloc of the matrix R.

Return Value

ColumnVector.

irotk

Syntax

ReturnMatrix irotk(const Matrix & R);

Description

Given a homogeneous transform matrix R, this function returns a column vector

[ ] k (2.5) θ

with k a unit vector such that the 3 × 3 rotation bloc of the matrix

Rot (k,θ) (2.6)

is equal to the 3 × 3 rotation bloc of the matrix R.

Return Value

ColumnVector.

irpy

Syntax

ReturnMatrix irpy(const Matrix & R);

Description

Given a homogeneous transform matrix R, this function returns a column vector

⌊ α ⌋ | | ⌈ β ⌉ (2.7) γ

such that the 3 × 3 rotation bloc of the matrix

Rot (z,γ)Rot (y, β)Rot (x,α ) (2.8)

is equal to the 3 × 3 rotation bloc of the matrix R.

Return Value

ColumnVector.

rotd

Syntax

ReturnMatrix rotd(const Real theta,
const ColumnVector & k1,
const ColumnVector & k2);

Description

This function returns the matrix of a rotation of an angle theta around the oriented line segment defined by the points k1 and k2.

Note: the column vectors k1 and k2 must have a length of at least 3. Only the first 3 elements are used.

Return Value

Matrix

rotk

Syntax

ReturnMatrix rotk(const Real theta,
const ColumnVector & k);

Description

This function returns the matrix of a rotation of an angle theta around the vector k.

Rot (k,θ) (2.9)

Note: the column vector k must have a length of at least 3. Only the first 3 elements are used.

Return Value

Matrix

rpy

Syntax

ReturnMatrix rpy(const ColumnVector & a);

Description

Given a column vector a

⌊ α ⌋ | β | (2.10) ⌈ ⌉ γ

this function returns the homogeneous transform matrix given by

Rot (z,γ)Rot (y, β)Rot (x,α ) (2.11)

Note: the column vector a must have a length of at least 3. Only the first 3 elements are used.

Return Value

Matrix

rotx, roty, rotz

Syntax

ReturnMatrix rotx(const Real alpha);
ReturnMatrix roty(const Real beta);
ReturnMatrix rotz(const Real gamma);

Description

These functions return the elementary rotation matrices:

⌊ ⌋ | 1 0 0 0 | Rot (x,α) = || 0 cosα - sin α 0 || (2.12) ⌈ 0 sin α cosα 0 ⌉ 0 0 0 1 ⌊ cos β 0 sin β 0 ⌋ | | Rot (y,β) = || 0 1 0 0 || (2.13) ⌈ - sin β 0 cosβ 0 ⌉ 0 0 0 1 ⌊ cosγ - sin γ 0 0 ⌋ | sin γ cosγ 0 0 | Rot (z,γ) = || || (2.14) ⌈ 0 0 1 0 ⌉ 0 0 0 1

Return Value

Matrix

trans

Syntax

ReturnMatrix trans(const ColumnVector & a);

Description

Given a column vector a, this function returns the following matrix:

⌊ 1 0 0 a ⌋ | 1 | T rans (a) = || 0 1 0 a2 || (2.15) ⌈ 0 0 1 a3 ⌉ 0 0 0 1

Note: the column vector a must have a length of at least 3. Only the first 3 elements are used.

Return Value

Matrix

[next] [front] [up]