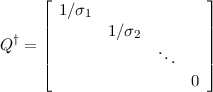[next] [prev] [prev-tail] [tail] [up]

2.18 Miscellaneous

odeint

Syntax
void odeint(ReturnMatrix (*xdot)(Real time, const Matrix & xin),  
            Matrix & xo,  
            Real to,  
            Real tf,  
            Real eps,  
            Real h1,  
            Real hmin,  
            int & nok,  
            int & nbad,  
            RowVector & tout,  
            Matrix & xout,  
            Real dtsav);

Description

This function performs the numerical integration of

˙x = f(x(t),t) (2.76)
using an adaptive step size based on 4th order Runge-Kutta scheme. It carries out the integration of xdot with the initial conditions given by xo, from time to to tf with accuracy eps saving the results at dtsav increments. After the function call, tout is set as
[ ] t0 t1 ⋅⋅⋅ tnsteps (2.77)
xout as
[ ] x0 x1 ⋅⋅⋅ xnsteps (2.78)
xo as xnsteps, nok and nbad to the number of good and bad steps taken. The function odeint is adapted from [18].

Return Value

None (xo, tout and xout are modified on output)

Runge_Kutta4

Syntax
void Runge_Kutta4(ReturnMatrix (*xdot)(Real time, const Matrix & xin),  
                  const Matrix & xo,  
                  Real to,  
                  Real tf,  
                  int nsteps,  
                  RowVector & tout,  
                  Matrix & xout);

Description

This function performs the numerical integration of

˙x = f(x(t),t) (2.79)
using a fixed step size 4th order Runge-Kutta scheme. It carries out the integration of xdot with the initial conditions given by xo, from time to to tf with nsteps. After the function call, tout is set as
[ ] t0 t1 ⋅⋅⋅ tnsteps (2.80)
and xout as
[ ] x0 x1 ⋅⋅⋅ xnsteps (2.81)

Return Value

None (tout and xout are modified on output)

Integ_Trap

Syntax
ReturnMatrix Integ_Trap(const ColumnVector & present, ColumnVector & past,  
                        Real dt);

Description

This function performs the trapezoidal integration of the vector past to vector present over dt.

Return Value

Matrix

pinv

Syntax
ReturnMatrix pinv(const Matrix & M);

Description

This function computes the pseudo inverse of the matrix M using SVD. If A = U*QV is a singular value decomposition of A, then A† = V *Q†U where X* is the conjugate transpose of X and

⌊ ⌋ | 1∕σ1 | Q † = || 1∕σ2 || |⌈ ... |⌉ 0
where the 1∕σi are replaced by 0 when 1∕σi < tol.

Return Value

Matrix

vec_dot_prod

Syntax
Real vec_dot_prod(const ColumnVector & x, const ColumnVector & y);

Description

This function performs the vector dot product on x and y.

Return Value

ColumnVector

x_prod_matrix

Syntax
ReturnMatrix x_prod_matrix(const ColumnVector & x);

Description

This function computes the cross product matrix S(x) of x such that S(x)y = x × y.

Return Value

Matrix

[next] [prev] [prev-tail] [front] [up]