Quaternion class definition. More...
#include <quaternion.h>
Public Member Functions | |
| Quaternion () | |
| Constructor. | |
| Quaternion (const Real angle_in_rad, const ColumnVector &axis) | |
| Constructor. | |
| Quaternion (const Real s, const Real v1, const Real v2, const Real v3) | |
| Constructor. | |
| Quaternion (const Matrix &R) | |
| Constructor. More... | |
| Quaternion | operator+ (const Quaternion &q) const |
| Overload + operator. More... | |
| Quaternion | operator- (const Quaternion &q) const |
| Overload - operator. More... | |
| Quaternion | operator* (const Quaternion &q) const |
| Overload * operator. More... | |
| Quaternion | operator/ (const Quaternion &q) const |
| Overload / operator. | |
| Quaternion | conjugate () const |
| Conjugate. More... | |
| Quaternion | i () const |
| Quaternion inverse.
where | |
| Quaternion & | unit () |
| Normalize a quaternion. | |
| Quaternion | exp () const |
| Exponential of a quaternion. More... | |
| Quaternion | power (const Real t) const |
| Quaternion | Log () const |
| Logarithm of a unit quaternion. More... | |
| Quaternion | dot (const ColumnVector &w, const short sign) const |
| Quaternion time derivative. More... | |
| ReturnMatrix | E (const short sign) const |
| Matrix E. More... | |
| Real | norm () const |
| Return the quaternion norm. More... | |
| Real | dot_prod (const Quaternion &q) const |
| Quaternion dot product. More... | |
| Real | s () const |
| Return scalar part. | |
| void | set_s (const Real s) |
| Set scalar part. | |
| ReturnMatrix | v () const |
| Return vector part. | |
| void | set_v (const ColumnVector &v) |
| Set vector part. More... | |
| ReturnMatrix | R () const |
| Rotation matrix from a unit quaternion. More... | |
| ReturnMatrix | T () const |
| Transformation matrix from a quaternion. More... | |
Private Attributes | |
| Real | s_ |
| Quaternion scalar part. | |
| ColumnVector | v_ |
| Quaternion vector part. | |
Detailed Description
Quaternion class definition.
Definition at line 89 of file quaternion.h.
Constructor & Destructor Documentation
| Quaternion::Quaternion | ( | const Matrix & | R | ) |
Constructor.
Cite_: Dam. The unit quaternion obtained from a matrix (see Quaternion::R())
![\[ R(s,v) = \left[ \begin{array}{ccc} s^2+v_1^2-v_2^2-v_3^2 & 2v_1v_2+2sv_3 & 2v_1v_3-2sv_2 \\ 2v_1v_2-2sv_3 & s^2-v_1^2+v_2^2-v_3^2 & 2v_2v_3+2sv_1 \\ 2v_1v_3+2sv_2 &2v_2v_3-2sv_1 & s^2-v_1^2-v_2^2+v_3^2 \end{array} \right] \]](form_125.png)
First we find 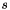 :
:
![\[ R_{11} + R_{22} + R_{33} + R_{44} = 4s^2 \]](form_127.png)
Now the other values are:
![\[ s = \pm \frac{1}{2}\sqrt{R_{11} + R_{22} + R_{33} + R_{44}} \]](form_128.png)
![\[ v_1 = \frac{R_{32}-R_{23}}{4s} \]](form_129.png)
![\[ v_2 = \frac{R_{13}-R_{31}}{4s} \]](form_130.png)
![\[ v_3 = \frac{R_{21}-R_{12}}{4s} \]](form_131.png)
The sign of 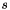 cannot be determined. Depending on the choice of the sign for s the sign of
cannot be determined. Depending on the choice of the sign for s the sign of 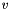 change as well. Thus the quaternions
change as well. Thus the quaternions 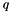 and
and 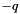 represent the same rotation, but the interpolation curve changed with the choice of the sign. A positive sign has been chosen.
represent the same rotation, but the interpolation curve changed with the choice of the sign. A positive sign has been chosen.
Definition at line 117 of file quaternion.cpp.
Member Function Documentation
| Quaternion Quaternion::conjugate | ( | ) | const |
| Quaternion Quaternion::dot | ( | const ColumnVector & | w, |
| const short | sign | ||
| ) | const |
Quaternion time derivative.
The quaternion time derivative, quaternion propagation equation, is
![\[ \dot{s} = - \frac{1}{2}v^Tw_{_0} \]](form_153.png)
![\[ \dot{v} = \frac{1}{2}E(s,v)w_{_0} \]](form_154.png)
![\[ E = sI - S(v) \]](form_155.png)
where 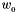 is the angular velocity vector expressed in the base frame. If the vector is expressed in the object frame,
is the angular velocity vector expressed in the base frame. If the vector is expressed in the object frame, 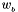 , the time derivative becomes
, the time derivative becomes
![\[ \dot{s} = - \frac{1}{2}v^Tw_{_b} \]](form_158.png)
![\[ \dot{v} = \frac{1}{2}E(s,v)w_{_b} \]](form_159.png)
![\[ E = sI + S(v) \]](form_160.png)
Definition at line 385 of file quaternion.cpp.
References s_, sign(), and v_.
Referenced by Impedance::control().
| Real Quaternion::dot_prod | ( | const Quaternion & | q | ) | const |
Quaternion dot product.
The dot product of quaternion is defined by
![\[ q_1\cdot q_2 = s_1s_2 + v_1 \cdot v_2 \]](form_161.png)
Definition at line 442 of file quaternion.cpp.
Referenced by Slerp(), Slerp_prime(), and Resolved_acc::torque_cmd().
| ReturnMatrix Quaternion::E | ( | const short | sign | ) | const |
Matrix E.
See Quaternion::dot for explanation.
Definition at line 423 of file quaternion.cpp.
References sign(), threebythreeident, and x_prod_matrix().
Referenced by Omega().
| Quaternion Quaternion::exp | ( | ) | const |
Exponential of a quaternion.
Let a quaternion of the form ![$q = [0, \theta v]$](form_149.png) , q is not necessarily a unit quaternion. Then the exponential function is defined by
, q is not necessarily a unit quaternion. Then the exponential function is defined by ![$q = [\cos(\theta),v \sin(\theta)]$](form_150.png) .
.
Definition at line 333 of file quaternion.cpp.
Referenced by Spl_Quaternion::quat(), and Spl_Quaternion::quat_w().
| Quaternion Quaternion::Log | ( | ) | const |
Logarithm of a unit quaternion.
The logarithm function of a unit quaternion ![$q = [\cos(\theta), v \sin(\theta)]$](form_151.png) is defined as
is defined as ![$log(q) = [0, v\theta]$](form_152.png) . The result is not necessary a unit quaternion.
. The result is not necessary a unit quaternion.
Definition at line 362 of file quaternion.cpp.
| Real Quaternion::norm | ( | ) | const |
Return the quaternion norm.
The norm of quaternion is defined by
![\[ N(q) = s^2 + v\cdot v \]](form_145.png)
Definition at line 295 of file quaternion.cpp.
| Quaternion Quaternion::operator* | ( | const Quaternion & | rhs | ) | const |
Overload * operator.
The multiplication of two quaternions is
![\[ q = q_1q_2 = [s_1s_2 - v_1\cdot v_2, v_1 \times v_2 + s_1v_2 + s_2v_1] \]](form_139.png)
where  and
and 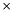 denote the scalar and vector product in
denote the scalar and vector product in 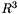 respectively.
respectively.
If 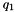 and
and 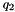 are unit quaternions, then q will also be a unit quaternion.
are unit quaternions, then q will also be a unit quaternion.
Definition at line 240 of file quaternion.cpp.
| Quaternion Quaternion::operator+ | ( | const Quaternion & | rhs | ) | const |
Overload + operator.
The quaternion addition is
![\[ q_1 + q_2 = [s_1, v_1] + [s_2, v_2] = [s_1+s_2, v_1+v_2] \]](form_135.png)
The result is not necessarily a unit quaternion even if 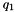 and
and 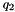 are unit quaternions.
are unit quaternions.
Definition at line 200 of file quaternion.cpp.
| Quaternion Quaternion::operator- | ( | const Quaternion & | rhs | ) | const |
Overload - operator.
The quaternion soustraction is
![\[ q_1 - q_2 = [s_1, v_1] - [s_2, v_2] = [s_1-s_2, v_1-v_2] \]](form_138.png)
The result is not necessarily a unit quaternion even if 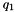 and
and 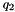 are unit quaternions.
are unit quaternions.
Definition at line 220 of file quaternion.cpp.
| ReturnMatrix Quaternion::R | ( | ) | const |
Rotation matrix from a unit quaternion.
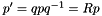 where
where 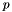 is a vector,
is a vector, 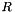 a rotation matrix and
a rotation matrix and 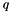 q quaternion. The rotation matrix obtained from a quaternion is then
q quaternion. The rotation matrix obtained from a quaternion is then
![\[ R(s,v) = (s^2 - v^Tv)I + 2vv^T - 2s S(v) \]](form_165.png)
![\[ R(s,v) = \left[ \begin{array}{ccc} s^2+v_1^2-v_2^2-v_3^2 & 2v_1v_2+2sv_3 & 2v_1v_3-2sv_2 \\ 2v_1v_2-2sv_3 & s^2-v_1^2+v_2^2-v_3^2 & 2v_2v_3+2sv_1 \\ 2v_1v_3+2sv_2 &2v_2v_3-2sv_1 & s^2-v_1^2-v_2^2+v_3^2 \end{array} \right] \]](form_125.png)
where 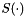 is the cross product matrix defined by
is the cross product matrix defined by
![\[ S(u) = \left[ \begin{array}{ccc} 0 & -u_3 & u_2 \\ u_3 &0 & -u_1 \\ -u_2 & u_1 & 0 \\ \end{array} \right] \]](form_167.png)
Definition at line 455 of file quaternion.cpp.
References threebythreeident, and x_prod_matrix().
Referenced by Dynamics::set_robot_on_first_point_of_splines().
| void Quaternion::set_v | ( | const ColumnVector & | v | ) |
Set vector part.
Set quaternion vector part.
Definition at line 271 of file quaternion.cpp.
Referenced by Integ_quat(), Integ_Trap_quat_v(), operator*(), and operator/().
| ReturnMatrix Quaternion::T | ( | ) | const |
Transformation matrix from a quaternion.
See Quaternion::R() for equations.
Definition at line 496 of file quaternion.cpp.
References fourbyfourident, and x_prod_matrix().
![\[ q^{-1} = \frac{q^{*}}{N(q)} \]](form_146.png)
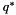 and
and 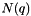 are the quaternion conjugate and the quaternion norm respectively.
are the quaternion conjugate and the quaternion norm respectively. ![$q = [s, v]$](form_143.png) is
is ![$q^{*} = [s, -v]$](form_144.png)
