#include <stewart.h>
Public Member Functions | |
| Stewart () | |
| Default Constructor. | |
| Stewart (const Matrix InitPlat, bool Joint=true) | |
| Constructor. More... | |
| Stewart (const Stewart &x) | |
| Copy Constructor. | |
| Stewart (const std::string &filename, const std::string &PlatformName) | |
| ~Stewart () | |
| Destructor. | |
| const Stewart & | operator= (const Stewart &x) |
| void | set_Joint (const bool _Joint) |
| Set the position of the universal joint on the links. | |
| void | set_q (const ColumnVector _q) |
| Set the position of the platform. | |
| void | set_dq (const ColumnVector _dq) |
| Set the platform's speed. | |
| void | set_ddq (const ColumnVector _ddq) |
| Set the platform's acceleration. | |
| void | set_pR (const ColumnVector _pR) |
| Set the position of the center of mass of the platform. | |
| void | set_pIp (const Matrix _pIp) |
| Set the inertia matrix of the platform. | |
| void | set_mp (const Real _mp) |
| Set the mass of the platform. | |
| bool | get_Joint () const |
| Return the position of the universal joint (true if at base, false if at platform) | |
| ReturnMatrix | get_q () const |
| Return the position of the platform. | |
| ReturnMatrix | get_dq () const |
| Return the speed of the platform. | |
| ReturnMatrix | get_ddq () const |
| Return the acceleration of the platform. | |
| ReturnMatrix | get_pR () const |
| Return the postion of the center of mass of the platfom. | |
| ReturnMatrix | get_pIp () const |
| Return the inertia matrix of the platform. | |
| Real | get_mp () const |
| Return the mass of the platform. | |
| void | Transform () |
| Call the functions corresponding to the basic parameters when q changes. More... | |
| ReturnMatrix | Find_wRp () |
| Return the rotation matrix wRp. More... | |
| ReturnMatrix | Find_Omega () |
| Return the angular speed of the platform. More... | |
| ReturnMatrix | Find_Alpha () |
| Return the angular acceleration of the platform. More... | |
| ReturnMatrix | jacobian () |
| Return the jacobian matrix of the platform. More... | |
| ReturnMatrix | Find_InvJacob1 () |
| Return the first intermediate jacobian matrix (reverse) of the platform. More... | |
| ReturnMatrix | Find_InvJacob2 () |
| Return the second intermediate jacobian matrix (reverse) of the platform. More... | |
| ReturnMatrix | jacobian_dot () |
| Return time deriative of the inverse jacobian matrix of the platform. More... | |
| ReturnMatrix | Find_dl () |
| Return the extension rate of the links in a vector. More... | |
| ReturnMatrix | Find_ddl () |
| Return the extension acceleration of the links in a vector. More... | |
| ReturnMatrix | Find_C (const Real Gravity=GRAVITY) |
| Return intermediate matrix C for the dynamics calculations. More... | |
| ReturnMatrix | Torque (const Real Gravity=GRAVITY) |
| Return the torque vector of the platform. More... | |
| ReturnMatrix | JointSpaceForceVct (const Real Gravity=GRAVITY) |
| Return a vector containing the six actuation force components. More... | |
| ReturnMatrix | InvPosKine () |
| Return the lenght of the links in a vector. More... | |
| ReturnMatrix | ForwardKine (const ColumnVector guess_q, const ColumnVector l_given, const Real tolerance=0.001) |
| Return the position vector of the platform (vector q) More... | |
| ReturnMatrix | Find_h (const Real Gravity=GRAVITY) |
| Return the intermediate matrix corresponding to the Coriolis and centrifugal + gravity force/torque components. More... | |
| ReturnMatrix | Find_M () |
| Return the intermediate matrix corresponding to the inertia matrix of the machine. More... | |
| ReturnMatrix | ForwardDyn (const ColumnVector Torque, const Real Gravity=GRAVITY) |
| Return the acceleration vector of the platform (ddq) More... | |
| void | Find_Mc_Nc_Gc (Matrix &Mc, Matrix &Nc, Matrix &Gc) |
| Return(!) the intermediates matrix for forward dynamics with actuator dynamics. More... | |
| ReturnMatrix | ForwardDyn_AD (const ColumnVector Command, const Real t) |
| Return the acceleration of the platform (Stewart platform mechanism dynamics including actuator dynamics) More... | |
Public Attributes | |
| Matrix | wRp |
| Rotation matrix describing the orientation of the platform. | |
| Matrix | Jacobian |
| Jacobian matrix. | |
| Matrix | IJ1 |
| Inverse of the first intermediate Jacobian matrix. | |
| Matrix | IJ2 |
| Inverse of the second intermediate Jacobian matrix. | |
| ColumnVector | dl |
| Rate of expension vector. | |
| ColumnVector | ddl |
| Acceleration of expension vector. | |
| ColumnVector | Alpha |
| Angular speed of the platform. | |
| ColumnVector | Omega |
| Angular acceleration of the platform. | |
Private Attributes | |
| bool | UJointAtBase |
| Gives the position of the universal joint (true if at base, false if at platform) | |
| ColumnVector | q |
| Platform position (xyz + euler angles) | |
| ColumnVector | dq |
| Platform speed. | |
| ColumnVector | ddq |
| Platform acceleration. | |
| ColumnVector | pR |
| Platform center of mass (in its own referential) | |
| ColumnVector | gravity |
| Gravity vector. | |
| Matrix | pIp |
| Platform Inertia (local ref.) | |
| Real | mp |
| Platform mass. | |
| Real | p |
| Pitch of the ballscrew (links) | |
| Real | n |
| Gear ratio (links motor) | |
| Real | Js |
| Moment of inertia (ballscrew) | |
| Real | Jm |
| Moment of inertia (motor) | |
| Real | bs |
| Viscous damping coefficient of the ballscrew. | |
| Real | bm |
| Viscous damping coefficient of the motor. | |
| Real | Kb |
| Motor back EMF. | |
| Real | L |
| Motor Inductance. | |
| Real | R |
| Motor armature resistance. | |
| Real | Kt |
| Motor torque. | |
| LinkStewart | Links [6] |
| Platform links. | |
Detailed Description
Constructor & Destructor Documentation
| Stewart::Stewart | ( | const Matrix | InitPlatt, |
| bool | Joint = true |
||
| ) |
Constructor.
- Parameters
-
InitPlatt,: Platform initialization matrix. Joint,: bool indicating where is the universal joint
Definition at line 850 of file stewart.cpp.
Member Function Documentation
| ReturnMatrix Stewart::Find_Alpha | ( | ) |
Return the angular acceleration of the platform.
Eq:
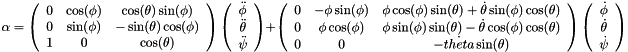
Where:
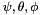 are the three Euler angles of the platform.
are the three Euler angles of the platform.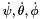 are the three Euler angle speed of the platform.
are the three Euler angle speed of the platform.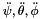 are the three Euler angle acceleration of the platform.
are the three Euler angle acceleration of the platform.
Definition at line 1258 of file stewart.cpp.
| ReturnMatrix Stewart::Find_C | ( | const Real | Gravity = GRAVITY | ) |
Return intermediate matrix C for the dynamics calculations.
Eqs:
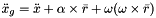
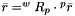
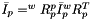
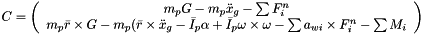
Where:
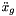 is the acceleration of the platform center of mass.
is the acceleration of the platform center of mass.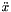 is the acceleration of the platform center (first three elements of the ddq vector).
is the acceleration of the platform center (first three elements of the ddq vector).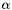 is the angular acceleration of the platform.
is the angular acceleration of the platform.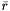 is the platform center of mass in the world referential.
is the platform center of mass in the world referential.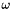 is the angular speed of the platform.
is the angular speed of the platform.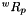 is the rotational matrix of the two referentials (world and platform).
is the rotational matrix of the two referentials (world and platform).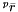 is the vector of the center of mass of the platform with reference to the local frame (platform).
is the vector of the center of mass of the platform with reference to the local frame (platform).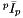 is the constant mass moments of inertia of the platform with reference to the local frame (platform).
is the constant mass moments of inertia of the platform with reference to the local frame (platform).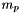 is the mass of the platform.
is the mass of the platform.- G is the gravity.
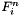 is the normal force transferred from the platform to the link.
is the normal force transferred from the platform to the link.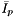 is the constant mass moments of inertia of the platform in the world referential.
is the constant mass moments of inertia of the platform in the world referential.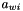 is the position of the attachment point of each link to the platform in the world referential.
is the position of the attachment point of each link to the platform in the world referential.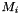 is the moment transferred from the platform to the link (not present is the spherical joint is at the platform end).
is the moment transferred from the platform to the link (not present is the spherical joint is at the platform end).
Definition at line 1509 of file stewart.cpp.
References Omega().
| ReturnMatrix Stewart::Find_ddl | ( | ) |
Return the extension acceleration of the links in a vector.
Eq:
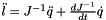
Where:
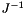 is the inverse jacobian matrix of the platform
is the inverse jacobian matrix of the platform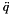 is the ddq vector
is the ddq vector
Definition at line 1469 of file stewart.cpp.
| ReturnMatrix Stewart::Find_dl | ( | ) |
Return the extension rate of the links in a vector.
Eq:
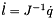
Where:
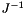 is the inverse Jacobian matrix of the platform
is the inverse Jacobian matrix of the platform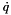 is the dq vector
is the dq vector
Definition at line 1448 of file stewart.cpp.
| ReturnMatrix Stewart::Find_h | ( | const Real | Gravity = GRAVITY | ) |
Return the intermediate matrix corresponding to the Coriolis and centrifugal + gravity force/torque components.
- Parameters
-
Gravity,: Gravity (9.81)
h is found by setting the ddq vector to zero and then calling the torque routine. The vector returned by Torque() is equal to h.
Definition at line 1643 of file stewart.cpp.
| ReturnMatrix Stewart::Find_InvJacob1 | ( | ) |
Return the first intermediate jacobian matrix (reverse) of the platform.
Eq:
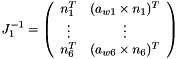
Where:
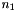 to
to 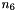 are the unit vector of the links
are the unit vector of the links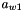 to
to 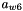 are the attachment point of the links to the platform in the world referential
are the attachment point of the links to the platform in the world referential
Definition at line 1313 of file stewart.cpp.
| ReturnMatrix Stewart::Find_InvJacob2 | ( | ) |
Return the second intermediate jacobian matrix (reverse) of the platform.
Eq:
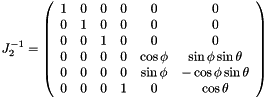
Where:
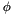 and
and 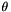 are two of the euler angle of the platform (vector q)
are two of the euler angle of the platform (vector q)
Definition at line 1341 of file stewart.cpp.
| ReturnMatrix Stewart::Find_M | ( | ) |
Return the intermediate matrix corresponding to the inertia matrix of the machine.
M is found by setting the dq and Gravity vectors to zero and the ddq vector to zero except for the ith element that is set to one. Then, the ith row of M is equal to the matrix returned by Torque().
Definition at line 1660 of file stewart.cpp.
| void Stewart::Find_Mc_Nc_Gc | ( | Matrix & | Mc, |
| Matrix & | Nc, | ||
| Matrix & | Gc | ||
| ) |
Return(!) the intermediates matrix for forward dynamics with actuator dynamics.
- Parameters
-
Mc,: Inertia matrix of the machine Nc,: Coriolis and centrifugal force/torque component Gc,: Gravity force/torque component
Eq:
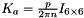
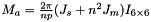
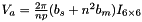
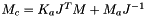
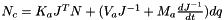
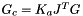 Where:
Where:
- p is the pitch of the ballscrew.
- n is the gear ratio.
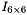 is the Identity matrix.
is the Identity matrix.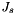 is the mass moment of inertia of the ballscrew.
is the mass moment of inertia of the ballscrew.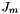 is the mass moment of inertia of the motor.
is the mass moment of inertia of the motor.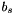 is the viscous damping coefficient of the ballscrew.
is the viscous damping coefficient of the ballscrew.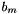 is the viscous damping coefficient of the motor.
is the viscous damping coefficient of the motor.- J is the Jacobian matrix of the platform.
Definition at line 1733 of file stewart.cpp.
| ReturnMatrix Stewart::Find_Omega | ( | ) |
Return the angular speed of the platform.
Eq:
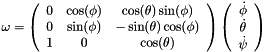
Where:
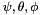 are the three Euler angles of the platform.
are the three Euler angles of the platform.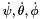 are the three Euler angle speed of the platform.
are the three Euler angle speed of the platform.
Definition at line 1220 of file stewart.cpp.
| ReturnMatrix Stewart::Find_wRp | ( | ) |
Return the rotation matrix wRp.
Eq of the matrix:
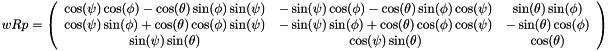
Where:
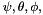 are the three Euler angles of the platform.
are the three Euler angles of the platform.
Definition at line 1183 of file stewart.cpp.
| ReturnMatrix Stewart::ForwardDyn | ( | const ColumnVector | T, |
| const Real | Gravity = GRAVITY |
||
| ) |
Return the acceleration vector of the platform (ddq)
- Parameters
-
T,: torque vector Gravity,: Gravity (9.81)
Eq:
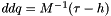
Where:
Definition at line 1698 of file stewart.cpp.
| ReturnMatrix Stewart::ForwardDyn_AD | ( | const ColumnVector | Command, |
| const Real | t | ||
| ) |
Return the acceleration of the platform (Stewart platform mechanism dynamics including actuator dynamics)
- Parameters
-
Command,: Vector of the 6 motors voltages. t,: period of time use to find the currents (di/dt)
Voltages with back emf:
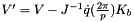
Currents:
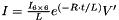
Motor torque:
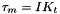
Platform acceleration:
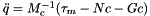
Where:
- J is the Jacobian matrix of the platform.
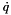 is the dq vector.
is the dq vector.- p is the pitch of the ballscrew.
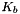 is the motor back emf constant.
is the motor back emf constant.- L is the motor armature inductance.
- R is the motor armature resistance.
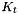 is the motor torque constant.
is the motor torque constant.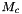 ,
, 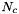 and
and 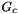 are from Find_Mc_Nc_Gc().
are from Find_Mc_Nc_Gc().
Definition at line 1789 of file stewart.cpp.
| ReturnMatrix Stewart::ForwardKine | ( | const ColumnVector | guess_q, |
| const ColumnVector | l_given, | ||
| const Real | tolerance = 0.001 |
||
| ) |
Return the position vector of the platform (vector q)
- Parameters
-
guess_q,: Approximation of real position l_given,: Lenght of the 6 links tolerance,: Ending criterion
The Newton-Raphson method is used to solve the forward kinematic problem. It is a numerical iterative technic that simplify the solution. An approximation of the answer has to be guess for this method to work.
Eq:
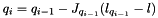
Where:
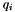 is the position vector of the platform at the ith iteration.
is the position vector of the platform at the ith iteration.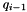 is the position vector of the platform at the (i-1)th iteration.
is the position vector of the platform at the (i-1)th iteration.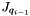 is the Jacobian matrix of the platform at the position of the
is the Jacobian matrix of the platform at the position of the 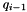 vector.
vector.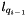 is the lenght vector of the links at the (i-1)th position of the platform.
is the lenght vector of the links at the (i-1)th position of the platform.- l is the real lenght vector of the links.
Definition at line 1564 of file stewart.cpp.
| ReturnMatrix Stewart::InvPosKine | ( | ) |
Return the lenght of the links in a vector.
The goal of the inverse kinematic is to find the lenght of each of the six links from the position of the platform (X,Y,Z, 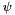 ,
, 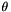 ,
, 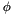 ).
).
Definition at line 1426 of file stewart.cpp.
| ReturnMatrix Stewart::jacobian | ( | ) |
Return the jacobian matrix of the platform.
Eq:
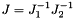
Where:
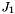 and
and 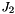 are intermediate matrix(Find_InvJacob1(), Find_InvJacob2())
are intermediate matrix(Find_InvJacob1(), Find_InvJacob2())
Definition at line 1287 of file stewart.cpp.
| ReturnMatrix Stewart::jacobian_dot | ( | ) |
Return time deriative of the inverse jacobian matrix of the platform.
Eq:
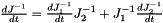
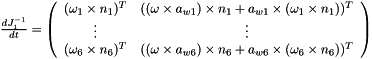
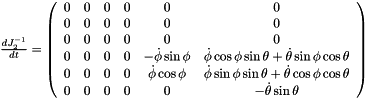
Where:
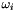 is the angular speed vector of each link
is the angular speed vector of each link- n is the unit vector of the link
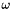 is the angular speed vector of the platform
is the angular speed vector of the platform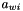 is the position vector of the attachment point of the link to the platform
is the position vector of the attachment point of the link to the platform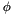 and
and 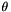 are two of the Euler angle (vector q)
are two of the Euler angle (vector q)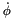 and
and 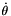 are two of the Euler angle speed (vector dq)
are two of the Euler angle speed (vector dq)
Definition at line 1386 of file stewart.cpp.
References Omega().
| ReturnMatrix Stewart::JointSpaceForceVct | ( | const Real | Gravity = GRAVITY | ) |
Return a vector containing the six actuation force components.
- Parameters
-
Gravity,: Gravity (9.81)
See the description of LinkStewart::ActuationForce().
Definition at line 1592 of file stewart.cpp.
| ReturnMatrix Stewart::Torque | ( | const Real | Gravity = GRAVITY | ) |
Return the torque vector of the platform.
- Parameters
-
Gravity,: Gravity (9.81)
Eq:
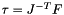
Where:
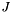 is the Jacobian matrix of the platform.
is the Jacobian matrix of the platform.- F is the joint space force vector (JointSpaceForceVct()).
Definition at line 1622 of file stewart.cpp.
| void Stewart::Transform | ( | ) |
Call the functions corresponding to the basic parameters when q changes.
These functions are called by Transform:
Definition at line 1157 of file stewart.cpp.
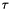 is the torque vector.
is the torque vector.