LinkStewart definitions. More...

#include <stewart.h>

Public Member Functions
	LinkStewart (const ColumnVector &InitLink, const Matrix wRp, const ColumnVector q)
	Constructor. More...

	LinkStewart (const LinkStewart &x)
	Copy constructor.

	LinkStewart ()
	Default Constructor.

	~LinkStewart ()
	Destructor.

const LinkStewart &	operator= (const LinkStewart &x)

void	set_ap (const ColumnVector NewAp)
	Set the position vector of platform attachment point.

void	set_b (const ColumnVector Newb)
	Set the position vector of the base attachment point.

void	set_I1aa (const Real NewI1aa)
	Set the value of inertia along the coaxial axis of part 1.

void	set_I1nn (const Real NewI1nn)
	Set the value of inertia along the tangent axis of part 1.

void	set_I2aa (const Real NewI2aa)
	Set the value of inertia along the coaxial axis of part 2.

void	set_I2nn (const Real NewI2nn)
	Set the value of inertia along the tangent axis of part 2.

void	set_m1 (const Real Newm1)
	Set the mass of part 1.

void	set_m2 (const Real Newm2)
	Set the mass of part 2.

void	set_Lenght1 (const Real NewLenght1)
	Set the lenght between platform attachment point and center of mass of part 1.

void	set_Lenght2 (const Real NewLenght2)
	Set the lenght between base attachment point and center of mass of part 2.

ReturnMatrix	get_ap () const
	Return the position vector of platform attachement point.

ReturnMatrix	get_b () const
	Return the position vector of base attachement point.

Real	get_I1aa () const
	Return the value of inertia along the coaxial axis of part 1.

Real	get_I1nn () const
	Return the value of inertia along the tangent axis of part 1.

Real	get_I2aa () const
	Return the value of inertia along the coaxial axis of part 2.

Real	get_I2nn () const
	Return the value of inertia along the tangent axis of part 2.

Real	get_m1 () const
	Return the mass of part 1.

Real	get_m2 () const
	Return the mass of part 2.

Real	get_Lenght1 () const
	Return the lenght between platform attachment point and center of mass of part 1.

Real	get_Lenght2 () const
	Return the lenght between base attachment point and center of mass of part 2.

void	LTransform (const Matrix wRp, const ColumnVector q)
	Recalculate the link's parameters related to the platform position. More...

void	d_LTransform (const ColumnVector dq, const ColumnVector Omega, const Real dl, const Real ddl)
	Recalculate the link's parameters related to the platform speed. More...

void	dd_LTransform (const ColumnVector ddq, const ColumnVector Omega, const ColumnVector Alpha, const Real dl, const Real ddl)
	Recalculate the link's parameters related to the platform acceleration. More...

void	tau_LTransform (const Real dl, const Real ddl, const Real Gravity)
	Recalculate the link's parameters related to the platform dynamics. More...

ReturnMatrix	Find_UnitV ()
	Return the unit vector of the link direction. More...

ReturnMatrix	Find_a (const Matrix _wRp, const ColumnVector _q)
	Return the position of the attachment point on the platform. More...

ReturnMatrix	Find_da (const ColumnVector dq, const ColumnVector Omega)
	Return the speed of the attachment point of the link on the platform. More...

ReturnMatrix	Find_dda (const ColumnVector ddq, const ColumnVector Omega, const ColumnVector Alpha)
	Return the acceleration of the attachment point of the link on the platform. More...

Real	Find_Lenght ()
	Return the lenght of the link. More...

ReturnMatrix	Find_VctU ()
	Return the unit vector of the universal joint along the first axis of the fixed revolute joint. More...

ReturnMatrix	Find_VctV ()
	Return the unit vector of the universal joint along the second axis of the fixed revolute joint. More...

ReturnMatrix	Find_VctC ()
	Return the unit vector of the universal joint along the third axis of the fixed revolute joint. More...

ReturnMatrix	Find_AngularKin (const Real dl, const Real ddl)
	Return the angular speed (Column 1) and angular acceleration (Column 2) of the link. More...

ReturnMatrix	NormalForce ()
	Return the normal component of the reaction force of the platform acting on the link. More...

ReturnMatrix	AxialForce (const Matrix J1, const ColumnVector C, const int Index)
	Return the axial component of the reaction force of the platform acting on the link. More...

ReturnMatrix	Find_N (const Real Gravity=GRAVITY)
	Return the intermediate matrix N for force calculation. More...

ReturnMatrix	Moment ()
	Return the moment component transmitted to the link from the base or the platform (depending where is the universal joint) More...

Real	ActuationForce (const Matrix J1, const ColumnVector C, const int Index, const Real Gravity=GRAVITY)
	Return the actuation force that power the prismatic joint. More...

ReturnMatrix	Find_ACM1 (const Real dl, const Real ddl)
	Return the acceleration of the center of mass of the first part of the link. More...

Public Attributes
ColumnVector	UnitV
	Unit Vector of the link.

ColumnVector	aPos
	Position of the platform attachment point.

ColumnVector	Vu
	Unit Vector of the universal joint (Rotational).

ColumnVector	Vc
	Unit Vector of the universal joint (Rotational).

ColumnVector	Vv
	Unit Vector of the universal joint (Rotational).

ColumnVector	da
	Speed of the platform attachment point .

ColumnVector	dda
	Acceleration of the platform attachment point.

ColumnVector	LOmega
	Angular speed of the link.

ColumnVector	LAlpha
	Angular acceleration of the link.

ColumnVector	ACM1
	Acceleration of the first center of mass.

ColumnVector	M
	Moment vector of the link.

ColumnVector	N
	Intermediate vector for dynamics calculations .

ColumnVector	gravity
	Gravity vector.

Real	L
	Lenght of the link.

Private Attributes
ColumnVector	ap
	Platform coordinates of the link in the local frame.

ColumnVector	b
	Base coordinates of the link int the global frame.

Real	I1aa
	Inertia along the coaxial axis for part 1.

Real	I1nn
	Inertia along the tangent axis for part 1.

Real	I2aa
	Inertia along the coaxial axis for part 2.

Real	I2nn
	Inertia along the tangent axis for part 2.

Real	m1
	Mass of part 1.

Real	m2
	Mass of part 2.

Real	Lenght1
	Lenght between the mass center (part 1) and the platform attachment.

Real	Lenght2
	Lenght between the mass center (part 2) and the base attachment.

Friends
class	Stewart

Detailed Description

LinkStewart definitions.

A Stewart platform is composed 6 links. This class describe the proprities of each of the platform's link.

Definition at line 50 of file stewart.h.

Constructor & Destructor Documentation

LinkStewart::LinkStewart	(	const ColumnVector &	InitLink,
		const Matrix	wRp,
		const ColumnVector	q
	)

Constructor.

Parameters

InitLink,:	LinkStewart initialization matrix.
wRp,:	Rotation matrix
q,:	Position of the platform

Definition at line 84 of file stewart.cpp.

Member Function Documentation

Real LinkStewart::ActuationForce	(	const Matrix	J1,
		const ColumnVector	C,
		const int	Index,
		const Real	Gravity = `GRAVITY`
	)

Return the actuation force that power the prismatic joint.

Parameters

J1,:	First intermidiate jacobian matrix (find with Stewart::Find_InvJacob1())
C,:	Intermidiate matrix in the dynamics calculation (find with Stewart::Find_C())
Index,:	Number of the link (1 to 6)
Gravity,:	Gravity (9.81)

Eq:

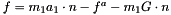
$f =m_1a_1\cdot{n}-f^a - m_1G\cdot{n}$

Where:

m_1 is the mass of the first part of the link
a_1 is the acceleration of the center of mass of the first part of the link
n is the unit vector of the link
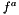is from LinkStewart::AxialForce
G is gravity

Definition at line 756 of file stewart.cpp.

ReturnMatrix LinkStewart::AxialForce	(	const Matrix	J1,
		const ColumnVector	C,
		const int	Index
	)

Return the axial component of the reaction force of the platform acting on the link.

Parameters

J1,:	First intermidiate jacobian matrix (find with Stewart::Find_InvJacob1())
C,:	Intermidiate matrix in the dynamics calculation (find with Stewart::Find_C())
Index,:	Number of the link (1 to 6)

Eq:

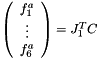
$\left( \begin{array}{c} f_1^a\\ \vdots\\ f_6^a\end{array} \right) = J_1^TC$

Where:

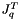is the jacobian matrix
C is an intermediate matrix (Stewart::Find_C())

Definition at line 724 of file stewart.cpp.

void LinkStewart::d_LTransform	(	const ColumnVector	dq,
		const ColumnVector	Omega,
		const Real	dl,
		const Real	ddl
	)

Recalculate the link's parameters related to the platform speed.

Parameters

dq,:	Speed of the platform.
Omega,:	Agular speed of the platform.
dl,:	Extension rate of the link.
ddl,:	Extension acceleration of the link.

Definition at line 326 of file stewart.cpp.

void LinkStewart::dd_LTransform	(	const ColumnVector	ddq,
		const ColumnVector	Omega,
		const ColumnVector	Alpha,
		const Real	dl,
		const Real	ddl
	)

Recalculate the link's parameters related to the platform acceleration.

Parameters

ddq,:	Acceleration of the platform.
Omega,:	Angular speed of the platform.
Alpha,:	Angular acceleration of the platform.
dl,:	Extension rate of the link.
ddl,:	Extension acceleration of the link.

Definition at line 344 of file stewart.cpp.

ReturnMatrix LinkStewart::Find_a	(	const Matrix	wRp,
		const ColumnVector	q
	)

Return the position of the attachment point on the platform.

Parameters

wRp,:	Rotation matrix.
q,:	Position of the platform.

The position of the attachment point on the platform is equal to the position of the center of the platform plus the position of the attach (in the local referencial) multiplicated by the rotation matrix:

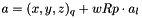
$a = (x,y,z)_q + wRp \cdot a_l$

where:

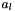is the position of the attach in the local referencial
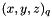is the position of the platform center (first 3 elements of the q vector)

Definition at line 375 of file stewart.cpp.

ReturnMatrix LinkStewart::Find_ACM1	(	const Real	dl,
		const Real	ddl
	)

Return the acceleration of the center of mass of the first part of the link.

Parameters

dl,:	Extention rate of the link
ddl,:	Extention acceleration of the link

Eq:

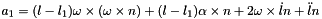
$a_1 = (l-l_1)\omega\times{(\omega\times{n})}+(l-l_1)\alpha\times{n}+2\omega\times{\dot{l}n}+\ddot{l}n$

Where:

l is the lenght of the link
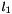is the distance between the center of mass of the first part of the link to the base
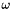$\omega$ is the angular speed of the link
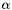$\alpha$ is the angular acceleration of the link
n is the unit vector of the link
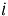$\dot{l}$ is the extension rate of the link
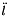$\ddot{l}$ is the extension acceleration of the link

Definition at line 799 of file stewart.cpp.

ReturnMatrix LinkStewart::Find_AngularKin	(	const Real	dl,
		const Real	ddl
	)

Return the angular speed (Column 1) and angular acceleration (Column 2) of the link.

Parameters

dl,:	Extention rate of the link
ddl,:	Extention acceleration of the link

Eqs for angular speed:

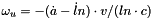
$\omega_u = -(\dot{a} - \dot{l}n)\cdot{v}/(ln\cdot{c})$

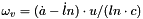
$\omega_v = (\dot{a}-\dot{l}n)\cdot{u}/(ln\cdot{c})$

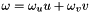
$\omega = \omega_u u + \omega_v v$

Eqs for angular acceleration:

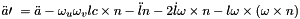
$\ddot{a}\prime\ = \ddot{a}-\omega_u\omega_v lc \times n - \ddot{l}n - 2\dot{l}\omega\times n - l\omega\times(\omega\times n)$

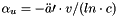
$\alpha_u = -\ddot{a}\prime\cdot{v}/(ln\cdot{c})$

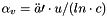
$\alpha_v = \ddot{a}\prime\cdot{u}/(ln\cdot{c})$

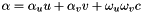
$\alpha = \alpha_u u + \alpha_v v +\omega_u\omega_vc$

where:

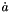$\dot{a}$ is the speed of the attachment point of the link to the platform
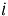$\dot{l}$ is the extension rate of the link
n is the unit vector of the link
l is the lenght of the link
u, v, c are the rot. vectors of the universal joint

Definition at line 582 of file stewart.cpp.

ReturnMatrix LinkStewart::Find_da	(	const ColumnVector	dq,
		const ColumnVector	Omega
	)

Return the speed of the attachment point of the link on the platform.

Parameters

dq,:	Speed of the platform
Omega,:	Angular speed of the platform

This function represent the equation: 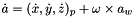$\dot{a} = (\dot{x},\dot{y},\dot{z})_p + \omega \times a_w$

Where:

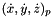$(\dot{x},\dot{y},\dot{z})_p$ is the speed of the platform center (first 3 elements of dq vector)
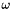$\omega$ is the angular speed of the platform
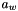is the position of the attachment point of the link to the platform in the world referential

Definition at line 435 of file stewart.cpp.

ReturnMatrix LinkStewart::Find_dda	(	const ColumnVector	ddq,
		const ColumnVector	Omega,
		const ColumnVector	Alpha
	)

Return the acceleration of the attachment point of the link on the platform.

Parameters

ddq,:	Acceleration of the platform.
Omega,:	Angular speed of the platform.
Alpha,:	Angular acceleration of the platform

This function represent the equation: 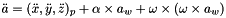$\ddot{a} = (\ddot{x},\ddot{y},\ddot{z})_p + \alpha \times a_w + \omega\times(\omega\times a_w)$

Where:

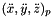$(\ddot{x},\ddot{y},\ddot{z})_p$ is the acceleration of the platform center (first 3 elements of ddq vector)
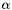$\alpha$ is the angular acceleration of the platform
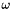$\omega$ is the angular speed of the platform
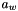is the position of the attachment point of the link to the platform in the world referential

Definition at line 461 of file stewart.cpp.

Real LinkStewart::Find_Lenght ( )

Return the lenght of the link.

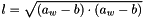
$l = \sqrt{(a_w - b)\cdot(a_w - b)}$

where:

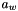is the position of the attachment point of the link to the platform in the world referential
b is the attachment point of the link to the base

Definition at line 483 of file stewart.cpp.

ReturnMatrix LinkStewart::Find_N ( const Real Gravity = GRAVITY )

Return the intermediate matrix N for force calculation.

Parameters

Gravity,: Gravity (9.81)

Eqs:

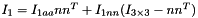
$I_1 = I_{1aa}nn^{T} + I_{1nn}(I_{3\times3}-nn^T)$

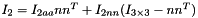
$I_2 = I_{2aa}nn^{T} + I_{2nn}(I_{3\times3}-nn^T)$

$N = -m_1(l-l_1)n\times{G}-m_2l_2(n\times{G})+(I_1+I_2)\alpha-(I_1+I_2)\omega\times{\omega}+m_1(l-l_1)n\times{a_1}+m_2l_2n\times{a_2}$

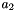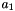Eq for $a_2$ ( $a_1$ is found with the Find_ACM1 function):

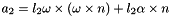
$a_2 = l_2\omega\times{(\omega\times{n})}+l_2\alpha\times{n}$

Where:

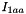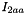$I_{1aa}$ and $I_{2aa}$ are the mass moment of inertia component about the main axis of the two parts of the link
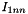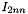$I_{1nn}$ and $I_{2nn}$ are the mass moment of inertia component about the normal axis of the two parts of the link
n is the unit vector of the link
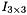$I_{3\times3}$ is a identity matrix
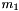is the mass of the first part of the link
l is the lenght of the link
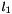is the distance between the center of mass of the first part of the link and the base
G is the gravity
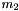is the mass of the second part of the link
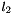is the distance between the center of mass of the second part of the link and the platform
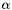$\alpha$ is the angular acceleration of the link
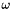$\omega$ is the angular speed of the link
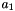and 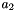are the acceleration of the center of mass of the two parts of the links

Definition at line 638 of file stewart.cpp.

ReturnMatrix LinkStewart::Find_UnitV ( )

Return the unit vector of the link direction.

The unit vector representing the orientation of the link is equal to:

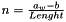
$n = \frac{a_w - b}{Lenght}$

where:

A is the position of the attachment point on the platform (world referential).
B is the position of the attachment point on the base (world referential).
Lenght is the lenght of the link.

Definition at line 413 of file stewart.cpp.

ReturnMatrix LinkStewart::Find_VctC ( )

Return the unit vector of the universal joint along the third axis of the fixed revolute joint.

Eq:

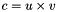
$c= u \times v$

Where:

u is the unit vector of the universal joint along the first axis of the fixed revolute joint
v is the unit vector of the universal joint along the second axis of the fixed revolute joint

Definition at line 545 of file stewart.cpp.

ReturnMatrix LinkStewart::Find_VctU ( )

Return the unit vector of the universal joint along the first axis of the fixed revolute joint.

This vector is equal to the unitary projection of the link unit vector on the X-Z plane:

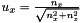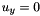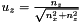
$u_x = \frac{n_x}{\sqrt{n_x^2+n_z^2}}$ ; $ u_y =0 $ ; $u_z = \frac{n_z}{\sqrt{n_x^2+n_z^2}}$

where:

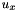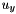, and 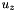are the elements of the vector
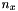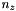and are the x component and the z component of the link unit vector

Definition at line 500 of file stewart.cpp.

ReturnMatrix LinkStewart::Find_VctV ( )

Return the unit vector of the universal joint along the second axis of the fixed revolute joint.

Eq:

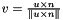
$v = \frac{u\times n}{\Vert u \times n \Vert}$

Where:

u is the unit vector of the universal joint along the first axis of the fixed revolute joint
n is the unit vector of the link

Definition at line 524 of file stewart.cpp.

void LinkStewart::LTransform	(	const Matrix	wRp,
		const ColumnVector	q
	)

Recalculate the link's parameters related to the platform position.

Parameters

wRp,:	rotation matrix.
q,:	Position of the platform.

Definition at line 312 of file stewart.cpp.

ReturnMatrix LinkStewart::Moment ( )

Return the moment component transmitted to the link from the base or the platform (depending where is the universal joint)

Eq:

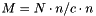
$M = N\cdot{n}/c\cdot{n}$

Where:

N is an intermediate matrix (Find_N)
n is the unit vector of the link
c is the rot. vector along the normal axis of the universal joint

Definition at line 663 of file stewart.cpp.

ReturnMatrix LinkStewart::NormalForce ( )

Return the normal component of the reaction force of the platform acting on the link.

Eq:

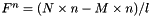
$F^n = (N\times{n} - M\times{n})/l$

Where:

N is an intermediate matrix (Find_N())
n is the unit vector of the link
M is the reaction moment on the link (Moment())
l is the lenght of the link

Definition at line 684 of file stewart.cpp.

const LinkStewart & LinkStewart::operator= ( const LinkStewart & x )

Overload = operator.

Definition at line 156 of file stewart.cpp.

References ACM1, ap, aPos, b, da, dda, gravity, I1aa, I1nn, I2aa, I2nn, L, LAlpha, Lenght1, Lenght2, LOmega, m1, m2, N, UnitV, Vc, Vu, and Vv.

void LinkStewart::tau_LTransform	(	const Real	dl,
		const Real	ddl,
		const Real	Gravity
	)

Recalculate the link's parameters related to the platform dynamics.

Parameters

dl,:	Extension rate of the link.
ddl,:	Extension acceleration of the link.
Gravity,:	Gravity (9.81).

Definition at line 363 of file stewart.cpp.

Public Member Functions

Public Attributes

Private Attributes

Friends

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation