Quaternion class. More...
#include "robot.h"Go to the source code of this file.
Classes | |
| class | Quaternion |
| Quaternion class definition. More... | |
Macros | |
| #define | BASE_FRAME 0 |
| #define | BODY_FRAME 1 |
| #define | EPSILON 0.0000001 |
Functions | |
| Quaternion | operator* (const Real c, const Quaternion &rhs) |
| Overload * operator, multiplication by a scalar. More... | |
| Quaternion | operator* (const Quaternion &lhs, const Real c) |
| Overload * operator, multiplication by a scalar. | |
| Quaternion | operator/ (const Real c, const Quaternion &rhs) |
| Overload / operator, division by a scalar. More... | |
| Quaternion | operator/ (const Quaternion &lhs, const Real c) |
| ReturnMatrix | Omega (const Quaternion &q, const Quaternion &q_dot) |
| Return angular velocity from a quaternion and it's time derivative. More... | |
| short | Integ_quat (Quaternion &dquat_present, Quaternion &dquat_past, Quaternion &quat, const Real dt) |
| Trapezoidal quaternion integration. | |
| Real | Integ_Trap_quat_s (const Quaternion &present, Quaternion &past, const Real dt) |
| Trapezoidal quaternion scalar part integration. | |
| ReturnMatrix | Integ_Trap_quat_v (const Quaternion &present, Quaternion &past, const Real dt) |
| Trapezoidal quaternion vector part integration. | |
| Quaternion | Slerp (const Quaternion &q0, const Quaternion &q1, const Real t) |
| Spherical Linear Interpolation. More... | |
| Quaternion | Slerp_prime (const Quaternion &q0, const Quaternion &q1, const Real t) |
| Spherical Linear Interpolation derivative. More... | |
| Quaternion | Squad (const Quaternion &p, const Quaternion &a, const Quaternion &b, const Quaternion &q, const Real t) |
| Spherical Cubic Interpolation. More... | |
| Quaternion | Squad_prime (const Quaternion &p, const Quaternion &a, const Quaternion &b, const Quaternion &q, const Real t) |
| Spherical Cubic Interpolation derivative. More... | |
Detailed Description
Quaternion class.
Definition in file quaternion.h.
Function Documentation
| ReturnMatrix Omega | ( | const Quaternion & | q, |
| const Quaternion & | q_dot | ||
| ) |
Return angular velocity from a quaternion and it's time derivative.
See Quaternion::dot for explanation.
Definition at line 557 of file quaternion.cpp.
References Quaternion::E(), and Quaternion::v().
Referenced by Stewart::Find_C(), Stewart::jacobian_dot(), Spl_Quaternion::quat_w(), Stewart::set_ddq(), and Stewart::set_dq().
| Quaternion operator* | ( | const Real | c, |
| const Quaternion & | q | ||
| ) |
Overload * operator, multiplication by a scalar.
![$q = [s, v]$](form_143.png) and let
and let 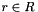 . Then
. Then ![$rq = qr = [r, 0][s, v] = [rs, rv]$](form_169.png)
The result is not necessarily a unit quaternion even if 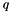 is a unit quaternions.
is a unit quaternions.
Definition at line 513 of file quaternion.cpp.
References Quaternion::s(), Quaternion::set_s(), Quaternion::set_v(), and Quaternion::v().
Referenced by operator*().
| Quaternion operator/ | ( | const Real | c, |
| const Quaternion & | q | ||
| ) |
Overload / operator, division by a scalar.
Same explanation as multiplication by scaler.
Definition at line 539 of file quaternion.cpp.
References Quaternion::s(), Quaternion::set_s(), Quaternion::set_v(), and Quaternion::v().
| Quaternion Slerp | ( | const Quaternion & | q0, |
| const Quaternion & | q1, | ||
| const Real | t | ||
| ) |
Spherical Linear Interpolation.
Cite_:Dam
The quaternion 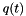 interpolate the quaternions
interpolate the quaternions 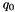 and
and 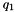 given the parameter
given the parameter 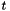 along the quaternion sphere.
along the quaternion sphere.
![\[ q(t) = c_0(t)q_0 + c_1(t)q_1 \]](form_173.png)
where 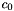 and
and 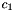 are real functions with
are real functions with 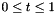 . As
. As 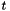 varies between 0 and 1. the values
varies between 0 and 1. the values 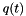 varies uniformly along the circular arc from
varies uniformly along the circular arc from 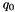 and
and 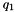 . The angle between
. The angle between 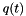 and
and 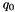 is
is 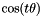 and the angle between
and the angle between 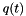 and
and 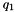 is
is 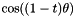 . Taking the dot product of
. Taking the dot product of 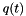 and
and 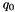 yields
yields
![\[ \cos(t\theta) = c_0(t) + \cos(\theta)c_1(t) \]](form_179.png)
and taking the dot product of 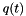 and
and 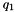 yields
yields
![\[ \cos((1-t)\theta) = \cos(\theta)c_0(t) + c_1(t) \]](form_180.png)
These are two equations with 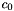 and
and 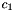 . The solution is
. The solution is
![\[ c_0 = \frac{\sin((1-t)\theta)}{\sin(\theta)} \]](form_181.png)
![\[ c_1 = \frac{\sin(t\theta)}{sin(\theta)} \]](form_182.png)
The interpolation is then
![\[ Slerp(q_0, q_1, t) = \frac{q_0\sin((1-t)\theta)+q_1\sin(t\theta)}{\sin(\theta)} \]](form_183.png)
If 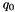 and
and 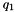 are unit quaternions the
are unit quaternions the 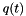 is also a unit quaternions. For unit quaternions we have
is also a unit quaternions. For unit quaternions we have
![\[ Slerp(q_0, q_1, t) = q_0(q_0^{-1}q_1)^t \]](form_184.png)
For t = 0 and t = 1 we have
![\[ q_0 = Slerp(q_0, q_1, 0) \]](form_185.png)
![\[ q_1 = Slerp(q_0, q_1, 1) \]](form_186.png)
It is customary to choose the sign G on q1 so that q0.Gq1 >=0 (the angle between q0 ang Gq1 is acute). This choice avoids extra spinning caused by the interpolated rotations.
Definition at line 628 of file quaternion.cpp.
References Quaternion::dot_prod(), and Quaternion::i().
Referenced by Spl_Quaternion::quat(), Spl_Quaternion::quat_w(), Slerp_prime(), Squad(), and Squad_prime().
| Quaternion Slerp_prime | ( | const Quaternion & | q0, |
| const Quaternion & | q1, | ||
| const Real | t | ||
| ) |
Spherical Linear Interpolation derivative.
Cite_: Dam
The derivative of the function 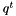 where
where 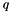 is a constant unit quaternion is
is a constant unit quaternion is
![\[ \frac{d}{dt}q^t = q^t log(q) \]](form_188.png)
Using the preceding equation the Slerp derivative is then
![\[ Slerp'(q_0, q_1, t) = q_0(q_0^{-1}q_1)^t log(q_0^{-1}q_1) \]](form_189.png)
It is customary to choose the sign G on q1 so that q0.Gq1 >=0 (the angle between q0 ang Gq1 is acute). This choice avoids extra spinning caused by the interpolated rotations. The result is not necessary a unit quaternion.
Definition at line 689 of file quaternion.cpp.
References Quaternion::dot_prod(), Quaternion::i(), and Slerp().
Referenced by Spl_Quaternion::quat_w().
| Quaternion Squad | ( | const Quaternion & | p, |
| const Quaternion & | a, | ||
| const Quaternion & | b, | ||
| const Quaternion & | q, | ||
| const Real | t | ||
| ) |
Spherical Cubic Interpolation.
Cite_: Dam
Let four quaternions be 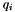 (p),
(p), 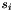 (a),
(a), 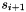 (b) and
(b) and 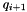 (q) be the ordered vertices of a quadrilateral. Obtain c from
(q) be the ordered vertices of a quadrilateral. Obtain c from 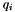 to
to 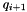 interpolation. Obtain d from
interpolation. Obtain d from 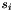 to
to 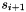 interpolation. Obtain e, the final result, from c to d interpolation.
interpolation. Obtain e, the final result, from c to d interpolation.
![\[ Squad(q_i, s_i, s_{i+1}, q_{i+1}, t) = Slerp(Slerp(q_i,q_{i+1},t),Slerp(s_i,s_{i+1},t), 2t(1-t)) \]](form_194.png)
The intermediate quaternion 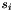 and
and 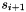 are given by
are given by
![\[ s_i = q_i exp\Big ( - \frac{log(q_i^{-1}q_{i+1}) + log(q_i^{-1}q_{i-1})}{4}\Big ) \]](form_195.png)
Definition at line 722 of file quaternion.cpp.
References Slerp().
Referenced by Spl_Quaternion::quat(), and Spl_Quaternion::quat_w().
| Quaternion Squad_prime | ( | const Quaternion & | p, |
| const Quaternion & | a, | ||
| const Quaternion & | b, | ||
| const Quaternion & | q, | ||
| const Real | t | ||
| ) |
Spherical Cubic Interpolation derivative.
Cite_: www.magic-software.com
The derivative of the function 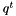 where
where 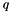 is a constant unit quaternion is
is a constant unit quaternion is
![\[ \frac{d}{dt}q^t = q^t log(q) \]](form_188.png)
Recalling that ![$log(q) = [0, v\theta]$](form_152.png) (see Quaternion::Log()). If the power is a function we have
(see Quaternion::Log()). If the power is a function we have
![\[ \frac{d}{dt}q^{f(t)} = f'(t)q^{f(t)}log(q) \]](form_196.png)
If 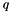 is a function of time and the power is differentiable function of time we have
is a function of time and the power is differentiable function of time we have
![\[ \frac{d}{dt}(q(t))^{f(t)} = f'(t)(q(t))^{f(t)}log(q) + f(t)(q(t))^{f(t)-1}q'(t) \]](form_197.png)
Using these last three equations Squad derivative can be define. Let 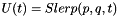 ,
, 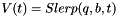 ,
, 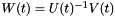 . We then have
. We then have 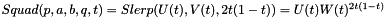
![\[ Squad'(p,a,b,q,t) = \frac{d}{dt}\Big [ UW^{2t(1-t)}\Big ] \]](form_202.png)
![\[ Squad'(p,a,b,q,t) = U\frac{d}{dt}\Big [ W^{2t(1-t)}\Big ] + U'\Big [W^{2t(1-t)}\Big] \]](form_203.png)
![\[ Squad'(p,a,b,q,t) = U\Big[(2-4t)W^{2t(1-t)}log(W)+2t(1-t)W^{2t(1-t)-1}W'\Big] + U'\Big[W^{2t(1-t)} \Big] \]](form_204.png)
where 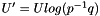 ,
, 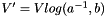 ,
, 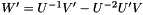
The result is not necessarily a unit quaternion even if all the input quaternions are unit.
Definition at line 748 of file quaternion.cpp.
References Quaternion::i(), and Slerp().
Referenced by Spl_Quaternion::quat_w().
