Impedance controller class. More...
#include <controller.h>
Public Member Functions | |
| Impedance () | |
| Constructor. | |
| Impedance (const Robot_basic &robot, const DiagonalMatrix &Mp_, const DiagonalMatrix &Dp_, const DiagonalMatrix &Kp_, const DiagonalMatrix &Mo_, const DiagonalMatrix &Do_, const DiagonalMatrix &Ko_) | |
| Constructor. | |
| short | set_Mp (const DiagonalMatrix &Mp_) |
Assign the translational impedance inertia matrix 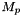 . More... . More... | |
| short | set_Mp (const Real MP_i, const short i) |
Assign the translational impedance inertia term 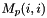 . More... . More... | |
| short | set_Dp (const DiagonalMatrix &Dp_) |
Assign the translational impedance damping matrix 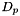 . More... . More... | |
| short | set_Dp (const Real Dp_i, const short i) |
Assign the translational impedance damping term 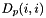 . More... . More... | |
| short | set_Kp (const DiagonalMatrix &Kp_) |
Assign the translational impedance stifness matrix 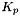 . More... . More... | |
| short | set_Kp (const Real Kp_i, const short i) |
Assign the translational impedance stifness term 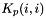 . More... . More... | |
| short | set_Mo (const DiagonalMatrix &Mo_) |
Assign the rotational impedance inertia matrix 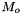 . More... . More... | |
| short | set_Mo (const Real Mo_i, const short i) |
Assign the rotational impedance inertia term 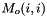 . More... . More... | |
| short | set_Do (const DiagonalMatrix &Do_) |
Assign the rotational impedance damping matrix 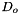 . More... . More... | |
| short | set_Do (const Real Do_i, const short i) |
Assign the rotational impedance damping term 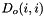 . More... . More... | |
| short | set_Ko (const DiagonalMatrix &Ko_) |
Assign the rotational impedance stifness matrix 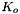 . More... . More... | |
| short | set_Ko (const Real Ko_i, const short i) |
Assign the rotational impedance stifness term 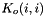 . More... . More... | |
| short | control (const ColumnVector &pdpp, const ColumnVector &pdp, const ColumnVector &pd, const ColumnVector &wdp, const ColumnVector &wd, const Quaternion &qd, const ColumnVector &f, const ColumnVector &n, const Real dt) |
| Generation of a compliance trajectory. More... | |
Public Attributes | |
| Quaternion | qc |
| Compliant frame quaternion. | |
| Quaternion | qcp |
| Compliant frame quaternion derivative. | |
| Quaternion | qcp_prev |
| Previous value of qcp. | |
| Quaternion | qcd |
| Orientation error (betweem compliant and desired frame) quaternion. | |
| Quaternion | quat |
| Temporary quaternion. | |
| ColumnVector | pc |
| Compliant position. | |
| ColumnVector | pcp |
| Compliant velocity. | |
| ColumnVector | pcpp |
| Compliant acceleration. | |
| ColumnVector | pcp_prev |
| Previous value of pcp. | |
| ColumnVector | pcpp_prev |
| Previous value of pcpp. | |
| ColumnVector | pcd |
| Difference between pc and desired position. | |
| ColumnVector | pcdp |
| Difference between pcp and desired velocity. | |
| ColumnVector | wc |
| Compliant angular velocity. | |
| ColumnVector | wcp |
| Compliant angular acceleration. | |
| ColumnVector | wcp_prev |
| Previous value of wcp. | |
| ColumnVector | wcd |
| Difference between wc and desired angular velocity. | |
Private Attributes | |
| DiagonalMatrix | Mp |
| Translational impedance inertia matrix. | |
| DiagonalMatrix | Dp |
| Translational impedance damping matrix. | |
| DiagonalMatrix | Kp |
| Translational impedance stifness matrix. | |
| DiagonalMatrix | Mo |
| Rotational impedance inertia matrix. | |
| DiagonalMatrix | Do |
| Rotational impedance damping matrix. | |
| DiagonalMatrix | Ko |
| Rotational impedance stifness matrix. | |
| Matrix | Ko_prime |
| Modified rotational impedance stifness matrix. | |
Detailed Description
Impedance controller class.
The implemantation of the impedance controller is made of two section: the first one is the generation of a compliance trajectory and the second one used a position controller to ensure the end effector follow the compliance trajectory (We recommended to used the resolve acceleration controller scheme, implemented in the class Resolved_acc).
This class generate a compliance path given by the translational and the rotational impedance.
![\[ M_p\ddot{\tilde{p}} + D_p\dot{\tilde{p}} + K_p\tilde{p} = f \]](form_30.png)
![\[ M_o\dot{\tilde{\omega}} + D_o\tilde{\omega} + K_o'\tilde{v} = n \]](form_31.png)
where 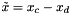 and
and 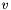 is the vector par of the quaternion representing the orientation error between the compliant and desired frame. The orientation error can also be express by rotation matrix,
is the vector par of the quaternion representing the orientation error between the compliant and desired frame. The orientation error can also be express by rotation matrix, 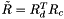 . The quaternion mathematics are implemented in the Quaternion class. The index
. The quaternion mathematics are implemented in the Quaternion class. The index  and
and 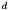 denote the compliance and the desired respectively.
denote the compliance and the desired respectively.
The impedance parameters 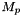 ,
, 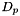 ,
, 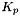 ,
, 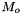 ,
, 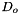 and
and 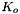 are
are 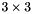 diagonal positive definite matrix
diagonal positive definite matrix
Definition at line 87 of file controller.h.
Member Function Documentation
| short Impedance::control | ( | const ColumnVector & | pdpp, |
| const ColumnVector & | pdp, | ||
| const ColumnVector & | pd, | ||
| const ColumnVector & | wdp, | ||
| const ColumnVector & | wd, | ||
| const Quaternion & | qd, | ||
| const ColumnVector & | f, | ||
| const ColumnVector & | n, | ||
| const Real | dt | ||
| ) |
Generation of a compliance trajectory.
- Parameters
-
pdpp,: desired end effector acceleration. pdp,: desired end effector velocity. pd,: desired end effector position. wdp,: desired end effector angular acceleration. wd,: desired end effector angular velocity. qd,: desired quaternion. f,: end effector contact force. n,: end effector contact moment. dt,: time frame.
- Returns
- short: 0 or WRONG_SIZE if one of the vector input is not
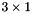 .
.
The translational and rotational impedance equations are integrated, with input 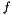 and
and 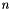 to computed
to computed 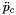 and
and 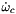 ,
, 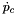 and
and 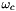 , and then
, and then 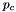 and
and 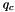 . The compliant quaternion
. The compliant quaternion 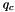 is obtained with the quaternion propagation equations (see Quaternion class).
is obtained with the quaternion propagation equations (see Quaternion class).
The quaternion -q represents exactly the same rotation as the quaternion q. The temporay quaternion, quat, is quatd plus a sign correction. It is customary to choose the sign G on q1 so that q0.Gq1 >=0 (the angle between q0 ang Gq1 is acute). This choice avoids extra spinning caused by the interpolated rotations.
Definition at line 294 of file controller.cpp.
References Quaternion::dot(), Quaternion::i(), Integ_quat(), Integ_Trap(), and WRONG_SIZE.
| short Impedance::set_Do | ( | const DiagonalMatrix & | Do_ | ) |
Assign the rotational impedance damping matrix 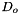 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
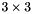 .
.
Definition at line 228 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Do | ( | const Real | Do_i, |
| const short | i | ||
| ) |
Assign the rotational impedance damping term 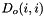 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
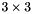 .
.
Definition at line 245 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Dp | ( | const DiagonalMatrix & | Dp_ | ) |
Assign the translational impedance damping matrix 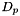 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
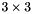 .
.
Definition at line 129 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Dp | ( | const Real | Dp_i, |
| const short | i | ||
| ) |
Assign the translational impedance damping term 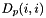 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
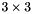 .
.
Definition at line 146 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Ko | ( | const DiagonalMatrix & | Ko_ | ) |
Assign the rotational impedance stifness matrix 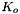 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
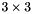 .
.
Definition at line 261 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Ko | ( | const Real | Ko_i, |
| const short | i | ||
| ) |
Assign the rotational impedance stifness term 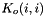 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
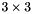 .
.
Definition at line 278 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Kp | ( | const DiagonalMatrix & | Kp_ | ) |
Assign the translational impedance stifness matrix 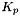 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
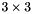 .
.
Definition at line 162 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Kp | ( | const Real | Kp_i, |
| const short | i | ||
| ) |
Assign the translational impedance stifness term 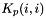 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
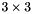 .
.
Definition at line 179 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Mo | ( | const DiagonalMatrix & | Mo_ | ) |
Assign the rotational impedance inertia matrix 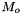 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
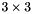 .
.
Definition at line 195 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Mo | ( | const Real | Mo_i, |
| const short | i | ||
| ) |
Assign the rotational impedance inertia term 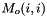 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
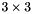 .
.
Definition at line 212 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Mp | ( | const DiagonalMatrix & | Mp_ | ) |
Assign the translational impedance inertia matrix 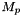 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
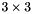 .
.
Definition at line 96 of file controller.cpp.
References WRONG_SIZE.
| short Impedance::set_Mp | ( | const Real | Mp_i, |
| const short | i | ||
| ) |
Assign the translational impedance inertia term 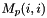 .
.
- Returns
- short: 0 or WRONG_SIZE if the matrix is not
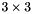 .
.
Definition at line 113 of file controller.cpp.
References WRONG_SIZE.
